Bismillah. Pertama kali saya mencoba kalman filter di Matlab, dulu saat kuliah, menggunakan Simulink dan M-File, cukup ribet sebenarnya [1]. Lalu, muncul request untuk membuat simulasi seluruhnya dengan M-File [2]. Kali ini pertanyaan yang ditujukan kepada saya adalah bagaimana membuat kalman filter diskrit dengan user-defined/embedded Matlab function dengan Simulink.
Sebagaimana dua tulisan sebelumnya, plant yang saya gunakan adalah pengukuran (diskrit) kecepatan motor dc dalam sinyal tegangan. Ulasan tentang plant dapat dilihat di sini [1]. Kalman filter diskrit di sini digunakan untuk estimasi, yaitu upaya pencarian nilai sejati dari nilai ukur yang bercampur noise.
Pertama, representasi sistem dalam state-space diskrit. Formulasi matematis dan penjelasannya ada di [1].
A=[0.7844 0.1116;0.5 0];
B=[1 0]';
H=[0.279 0.2936];
D=0;
Diagram Simulink
Sistem diskrit tersebut kira-kira dapat dinyatakan dalam diagram Simulink berikut.
Diagram Simulink
Sistem diskrit tersebut kira-kira dapat dinyatakan dalam diagram Simulink berikut.
Dalam diagram di atas, ada dua jenis noise yang diberikan, yaitu noise proses dan noise ukur. Dengan kata lain, z atau sinyal hasil pengukuran terdistorsi oleh kedua noise tersebut. Secara matematis, persamaan state-diskrit dari sistem di atas dinyatakan sebagai berikut.
x(k)=Ax(k-1)+Bu(k-1)+w(k-1)
z(k)=Hx(k-1)+v(k-1)
Tugas kalman filter adalah bagaimana dia sedapat mungkin mengeliminasi noise-noise tersebut sehingga didapatkan nilai y atau output sistem yang sebenarnya. Kalman filter diskrit dapat dibuat dengan menggunakan blok user-defined/embedded function di Simulink. Blok ini memungkinkan kita mendefinisikan fungsi kalman filter dengan kode matlab. Diagramnya kira-kira digambarkan sebagai berikut.
Input dari blok dekaef ada empat, dua diantaranya adalah feedback dari output sebelumnya, dua yang lain adalah z (sinyal ukur) dan u (input sistem). Nilai estimasi awal untuk state (x) dan kovarian error (P) didefinisikan di blok unit delay. Output zest adalah nilai estimasi sinyal ukur tanpa noise. Ringkasnya, kalman filter mengolah sinyal ukur yang bercampur noise menjadi sinyal ukur dengan noise seminimum mungkin.
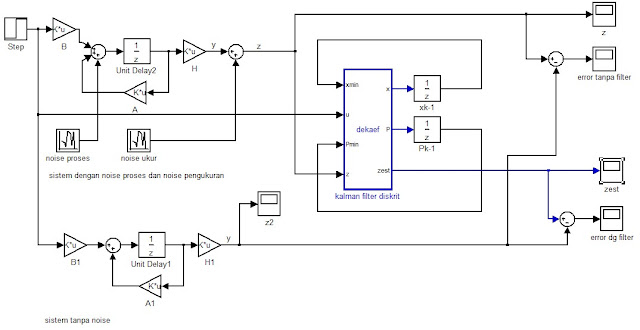

Diagram Simulink selengkapnya.
Fungsi MATLAB
Blok user-defined function diatas saya isi dengan kode berikut, sebagaimana algoritma kalman filter termaktub dalam pustaka [5].
Fungsi MATLAB
Blok user-defined function diatas saya isi dengan kode berikut, sebagaimana algoritma kalman filter termaktub dalam pustaka [5].
function [x,P,zest] = dekaef(xmin,u,Pmin,z)
Q=eye(2)*0.01;
R=eye(1)*0.1;
A=[0.7844 0.1116;0.5 0];
B=[1 0]';
H=[0.279 0.2936];
x=A*xmin+B*u;
P=A*Pmin*A'+Q;
K=P*H'*inv(H*P*H'+R);
x=x+K*(z-H*x);
P=(eye(2)-K*H)*P;
zest=H*x;
Tuning Parameter
Nilai parameter Q dan R menentukan kualitas estimasi kalman filter, setahu saya tidak ada rumus atau perhitungan tertentu untuk menentukan keduanya. Q adalah kovarian noise proses dan R adalah kovarian noise pengukuran. Menebak nilai Q pada dasarnya adalah menebak noise yang terlibat di dalam proses, makin dekat tebakan dengan nilai noise sebenarnya, makin bagus pula kualitas estimasi. Begitu juga dengan nilai R. Cerita dan uji coba tentang tuning parameter kalman filter pernah saya tuliskan di sini [2].
Ada satu perspektif menarik, khususnya terkait nilai R, bahwa pemilihan nilai R itu dikaitkan dengan seberapa percaya filter dengan sinyal ukur yang bercampur noise. Nilai R yang besar (misalnya R=1) membuat filter lebih lambat percaya terhadap sinyal ukur yang sedang diolahnya. Nilai R yang lebih kecil (misalnya R=0.001) membuat filter lebih cepat percaya terhadap sinyal ukur yang sedang diolahnya. Efeknya, pemilihan nilai R yang lebih besar, seringkali menghasilkan hasil estimasi yang lebih smooth. Cerita dan contoh lebih detil saya pernah tulis di sini [4].
Hasil Estimasi
Ada satu perspektif menarik, khususnya terkait nilai R, bahwa pemilihan nilai R itu dikaitkan dengan seberapa percaya filter dengan sinyal ukur yang bercampur noise. Nilai R yang besar (misalnya R=1) membuat filter lebih lambat percaya terhadap sinyal ukur yang sedang diolahnya. Nilai R yang lebih kecil (misalnya R=0.001) membuat filter lebih cepat percaya terhadap sinyal ukur yang sedang diolahnya. Efeknya, pemilihan nilai R yang lebih besar, seringkali menghasilkan hasil estimasi yang lebih smooth. Cerita dan contoh lebih detil saya pernah tulis di sini [4].
Hasil Estimasi
Karena keterbatasan waktu, saya tidak dapat cerita banyak dan tidak sempat uji coba untuk beberapa nilai Q dan R. Saya contohkan, pemilihan nilai Q=0.01 dan R=0.1. Kalman filter mampu mengolah sinyal z (kiri) yang bercampur noise menjadi sinyal zest (kanan). Nampak bahwa, noise telah banyak tereliminasi.
Saya tampilkan pula grafik errornya. Grafik sebelah kiri menampilkan perbedaan antara sinyal ukur z dengan sinyal output sistem tanpa noise (ideal). Grafik sebalah kanan menampilkan perbedaan antara sinyal ukur hasil estimasi zest dengan sinyal output sistem tanpa noise (ideal). Nampak bahwa, error dengan kalman filter jauh lebih minimum daripada error tanpa filter.
Kurang lebih demikian ini yang dapat saya ceritakan terkait kalman filter diskrit. Sesiapa yang sekiranya memerlukan file Simulinknya, silakan request via email: alfiyahibnumalik@gmail.com
atau WhatsApp 085733484101. Bila beruntung dan saya tidak lupa menemukan lokasi filenya, insya Allah akan saya kirimkan.
Versi pdf dari tulisan ini bisa diunduh di sini:
https://www.researchgate.net/publication/320696758_Membuat_Kalman_Filter_Diskrit_dengan_Simulink
Bila dirasa bermanfaat, mohon saya didoakan yang baik2. Mudah2an artikel ringkas ini bermanfaat. Aamiin. Alhamdulillah.
Referensi
atau WhatsApp 085733484101. Bila beruntung dan saya tidak lupa menemukan lokasi filenya, insya Allah akan saya kirimkan.
Versi pdf dari tulisan ini bisa diunduh di sini:
https://www.researchgate.net/publication/320696758_Membuat_Kalman_Filter_Diskrit_dengan_Simulink
Bila dirasa bermanfaat, mohon saya didoakan yang baik2. Mudah2an artikel ringkas ini bermanfaat. Aamiin. Alhamdulillah.
Referensi




No comments:
Post a Comment