Saya awali dokumen ini dengan Nama Alloh, Tuhan Semesta Alam, Sang Maha Pengasih dan Maha Penyayang
Download: [pdf] [program matlab] [referensi]
Abstrak
Sebagian besar Proses di industri fisika dan kimia adalah proses Multi Input Multi Output (MIMO), dan banyak diantaranya memiliki interaksi silang antar masing-masing input dan outputnya. Two Input Two Output (TITO) adalah contoh sederhana dari proses MIMO. Dibanding dengan Single Input Single Output (SISO), proses TITO lebih sulit dikendalikan karena terdapat interaksi silang antara variabel input dan outputnya.
Umumnya, terdapat dua metode dalam merancang kontroler untuk proses TITO. Pertama, metode modern, menggunakan kontroler terpusat/tunggal dan kedua, metode klasik, menggunakan kontroler terdesentralisasi.
Saya coba paparkan, dalam dokumen ini, bagaimana merancang kontroler Fuzzy-PI dengan teknik Decoupling untuk plant Coupled-Tank (TITO).
Plant Coupled-Tank
Berikut adalah foto dari Plant Coupled-Tank (1).
Gambar 1 Plant Coupled-Tank (1) (2)
Coupled-Tank dalam bahasan kita sekarang adalah contoh untuk proses TITO. Tujuannya adalah mengatur level/ketinggian air dalam dua tangki dengan dua pompa. Input dari plant ini adalah u1(t), u2(t) [tegangan input untuk pompa] dan output plant ini adalah h1(t), h2(t) [ketinggian air di tangki 1 dan tangki 2].
Dinamika plant ini dapat kita modelkan dengan persamaan diferensial berikut (1)
Persamaan 1 Model matematika Coupled Tank
Keterangan:
A = Luas penampang tangki 1 dan 2 (cm2),
a = luas penampang lubang keluaran tangki 1 dan 2 dan saluran penghubung antara tangki 1 dan 2 (cm2),
β1 dan β2 adalah rasio bukaan katup (valve) pada lubang keluaran tangki 1 dan 2,
βx adalah rasio valve antara tangki 1 dan tangki 2,
h1ss, h2ss adalah ketinggian air (steady-state) pada tangki 1 dan 2,
g adalah gravitasi (cm2/s) dan
k1, k2 penguatan (gain) pompa 1 dan 2 (cm3/V.s).
Persamaan 1 ini dapat ditransformasi ke dalam Matriks Transfer Function berikut. (1)
dimana
Persamaan 2 Matriks transfer function untuk Coupled-Tank
Keterangan:
h1ss, h2ss adalah ketinggian air (steady-state) pada tangki 1 dan 2,
T1 adalah konstanta waktu pada tangki 1,
T2 adalah konstanta waktu pada tangki 2, dan
Tx adalah konstanta waktu antara tangki 1 dan tangki 2.
Lalu kita tetapkan parameter dan titik kerja dari plant (1).
Tabel 1 Parameter Plant
| A (cm2) | 66.25 |
| a (cm2) | 0.1963 |
| β1 | 0.35903 |
| β2 | 0.45848 |
| βx | 0.38705 |
Tabel 2 Titik kerja dari Plant
| u1 (V) | 2.5 |
| u2 (V) | 2 |
| h1ss (x10% Range) | 2.749 |
| h2ss (x10% Range) | 3.262 |
| k1 (cm3/V.s) | 2.88 |
| k2 (cm3/V.s) | 2.588 |
Dengan mensubtitusikan nilai parameter dan titik kerja ini ke Persamaan 2, Kita dapatkan Matriks Transfer Function berikut.
Persamaan 3 Matriks transfer function dengan nilai parameter dan titik kerja (1)
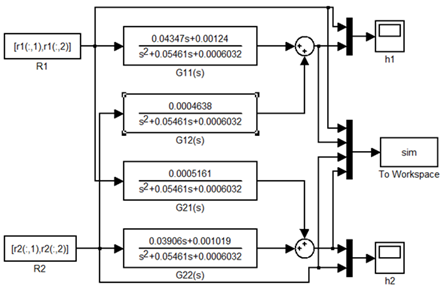
Matriks Transfer Function di atas direalisasikan dalam diagram blok berikut.
Gambar 2 Diagram blok Plant Coupled Tank (TITO) (1)
Decoupling
Plant Coupled-Tank memiliki dua input dan output yang punya pengaruh silang. Kita lihat pada Gambar 2, output h1(t) tidak hanya dipengaruhi oleh u1(t) tetapi juga dipengaruhi oleh u2(t), begitu juga dengan h2(t). Plant atau proses semacam ini dapat disederhanakan seakan-akan seperti proses Single Input Single Output (SISO) dengan teknik Decoupling. Decoupling mentransformasi model TITO ke dalam SISO untuk memudahkan analisis dan perancangan kontroler. Perhatikan Gambar 3.
Gambar 3 Diagram blok Plant dengan Decoupling (1)
dimana
Dengan menggunakan Matriks Transfer Function pada Persamaan 3, didapatkan bahwa
Kontroler 2-DOF Proportional-Integral (PI)
Numsomran, et.al (1) merancang kontroler 2-Degree of Freedom Proportional-Integral untuk mengendalikan Plant Coupled-Tank. Lihat Gambar 4. Decoupling mentransformasi proses Coupled-Tank (TITO) menjadi seolah-solah dua proses SISO yang independen. Di tiap SISO, karakteristirk sistem dianalisis dengan metode Root Locus untuk menentukan parameter kontroler PI.
Gambar 4 Desain Kontroler 2-DOF PI (1)
Untuk plant pada Persamaan 3, didapatkan kontroler feedback PI [C(s)] dan kontroler prefilter [F(s)] sebagaimana berikut.
Penjelasan selengkapnya, dapat Anda baca pada (1).
Kontroler Fuzzy-PI
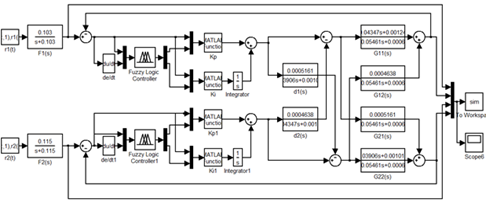
Diagram blok sistem pengaturan Coupled Tank dengan kontroler Fuzzy-PI ditampilkan pada Gambar 5. Proses dikendalikan dengan kontroler PI dan Fuzzy Logic bertugas mengatur parameter kontroler PI (tuning). Istilah variabel PI (pada Gambar) memiliki makna kontroler PI yang parameternya (Kp dan Ki) dapat diubah. Fuzzy Logic menerima dua input (sinyal error dan delta error) dan menghasilkan dua output (∆Kp dan ∆Ki).
Gambar 5 Diagram blok pengaturan tertutup dengan kontroler Fuzzy-PI (3)
Kontroler PI dibangun dengan persamaan kontinyu:
dimana nilai Kp dan Ki selalu diupdate dengan persamaan
Kp = Kp’ + ∆Kp dan Ki = Ki’ + ∆Ki, nilai ∆Kp dan ∆Ki didapat dari Fuzzy Logic. Kp’ dan Ki’ adalah Ki sebelum waktu ke-t.
Fuzzy Logic dibangun oleh tiga bagian penting:
1. Fuzzifikasi: mentransformasi nilai input ke dalam nilai linguistik. Terdapat dua variabel input, yaitu e(t) dan de(t)/dt. Masing-masing variabel input dipetakan ke dalam lima variabel linguistik dengan fungsi keanggotaan (Membership Function) Triangle, yaitu Negative Big (NB), Negative Small (NS), Zero (Z), Positive Small (PS), dan Positive Big (PB). Membership Function (MF) untuk variabel input dan output dapat dilihat pada Gambar 6 s.d. Gambar 9.
Gambar 6 Membership Function untuk Input 'error'
Gambar 7 Membership Function untuk input ‘de/dt'
Gambar 8 Membership Function untuk output '∆Kp'
Gambar 9 Membership Function untuk output '∆Ki'
2. Aturan Fuzzy: Tabel aturan yang menghubungkan variabel linguistik input dan output.
Tabel 3 Aturan Fuzzy untuk output Kp
Tabel 4 Aturan Fuzzy untuk output 'Ki'
3. Defuzzifikasi: mentransformasi nilai linguistik menjadi nilai output dengan metode Mamdani Centroid. Defuzzifikasi menghasilkan dua nilai output yaitu ∆Kp dan ∆Ki yang akan digunakan untuk mengupdate parameter kontroler PI.
Set-Poin untuk Simulasi
Dalam beberapa simulasi berikut, digunakan set-poin pada Tabel 5. Sinyal r1(t) dan r2(t) adalah sinyal tegangan listrik (dalam stauan Volt) yang mewakili ketinggian air yang diinginkan pada tangki 1 dan tangki 2.
Tabel 5 Set-point
| t = 0s | t = 100s | t = 300s | t = 400s | t = 500s | |
| r1(t) | 2 | 3 | 0 | 4 | 0 |
| r2(t) | 4 | 0 | 5 | 0 | 6 |
Simulasi 1: Respon Open Loop
Diagram Simulink untuk Simulasi Open Loop (file: openloop.mdl)
Respons Plant Coupled Tank Open Loop
Simulasi 2: Respon Closed Loop
Diagram Simulink untuk Simulasi Closed Loop (file: closedloop.mdl)
Respons Plant Coupled Tank Closed Loop
Simulasi 3: Closed Loop dengan Decoupling
Diagram Simulink untuk Simulasi Closed Loop dengan Decoupling (file: decoupling.mdl)
Respons Plant Closed Loop dengan Decoupling
Keterangan:
# Masih ada error steady-state
Simulasi 4: Closed Loop, Decoupling + Kontroler Proportional Integral (PI)
Diagram Simulink untuk Simulasi Closed Loop dengan Decoupling dan Kontroler 2-DOF PI (file: twodofpi.mdl)
Respons Plant Coupled Tank untuk Kontroler 2-DOF PI dengan Decoupling
Keterangan:
# Error steady-state nol
# Overshoot terjadi setiap pergantian set-point
Simulasi 5: Closed Loop, Decoupling + Kontroler Fuzzy-PI
Diagram Simulink untuk Simulasi Closed Loop dengan Decoupling dan Kontroler Fuzzy-PI (file: fuzzypi.mdl)
Respons Plant Coupled Tank untuk Kontroler Fuzzy-PI
Keterangan:
# Error steady-state nol
# Overshoot terjadi hanya pertama kali, di set-point pertama
Petunjuk Penggunaan Simulink Fuzzy-PI
1. Buka Matlab
2. Ubah Current Directory pada folder ‘nurq’
3. pada command window, ketik ‘setpoint’ lalu tekan enter
4. ketik ‘fuzzy’ lalu tekan enter, akan muncul kotak dialog FIS Editor
5. tekan ctrl+o (open), lalu pilih file ‘fuzzypi5.fis’
6. klik menu ‘File -> Save to workspace’, lalu keluar dari FIS Editor
7. tekan ctrl+o, lalu pilih file fuzzypi.mdl
8. jalankan simulasi
9. pada comman window, ketik ‘ploter’ lalu tekan enter
10. jika tidak ada masalah, maka akan muncul grafik
11. jika ingin menjalankan simulasi ini sekali lagi, pada command window, ketik ‘clearpersistent’ lalu tekan enter
12. jalankan simulasi sekali lagi (langkah 8)
Penutup
Sekian, Segala Puji Milik Alloh, Tuhan Semesta Alam
Daftar Pustaka
1. Design of 2-DOF PI Controller with Decoupling for Coupled-Tank Process. Numsomran, Arjin, Suksri, Tianchai and Thumma, Maitree. Seoul, Korea : s.n., 2007. International Conference on Control, Automation and Systems. p. 339.
2. Decentralized Fuzzy Logic Controller for TITO Coupled-Tank Process. Pornpatkul, Chatchaval and Suksri, Tianchai. Fukuoka, Japan : s.n., 2009. ICROS-SICE International Joint Conference.
3. Fuzzy Adaptive PID for Flow Control System based on OPC. Manjunath, R. Manoj and Raman, S. Janaki. 2011, IJCA Special Issue on "Computational Science - New Dimensions & Perspectives", p. 5.




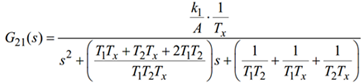






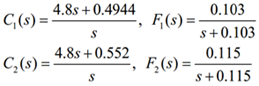















Bang admin, mau tanya dong. Couple tank itu apa si? Fungsinya buat apa? Terus pemodelannya itu bagaimana si bang? Ane masih ga paham bang sama rumus pemodelan mtknya. Kebetulan saya sedang ada tugas kampus terkait seperti jurnal abang ini. Tentang couple tank, bang mohon arahannya dong bang. Saya masih newbie bgt dalam dunia kontrol proses saya mau belajar bang.
ReplyDeleteCoupled tank itu dua tangki air yang saling terhubung di bawahnya. Konon banyak dijumpa di industri kimia dan makanan. Model matematiknya ada di persamaan dh1/dt dan dh2/dt. Trims
Delete